An exposition on the propriety of restricted Boltzmann machines

Andee Kaplan, Daniel Nordman, and Stephen Vardeman
Iowa State University
July 31, 2016
JSM - Chicago, IL
http://bit.ly/jsm2016-rbm

Andee Kaplan, Daniel Nordman, and Stephen Vardeman
Iowa State University
July 31, 2016
JSM - Chicago, IL
http://bit.ly/jsm2016-rbm
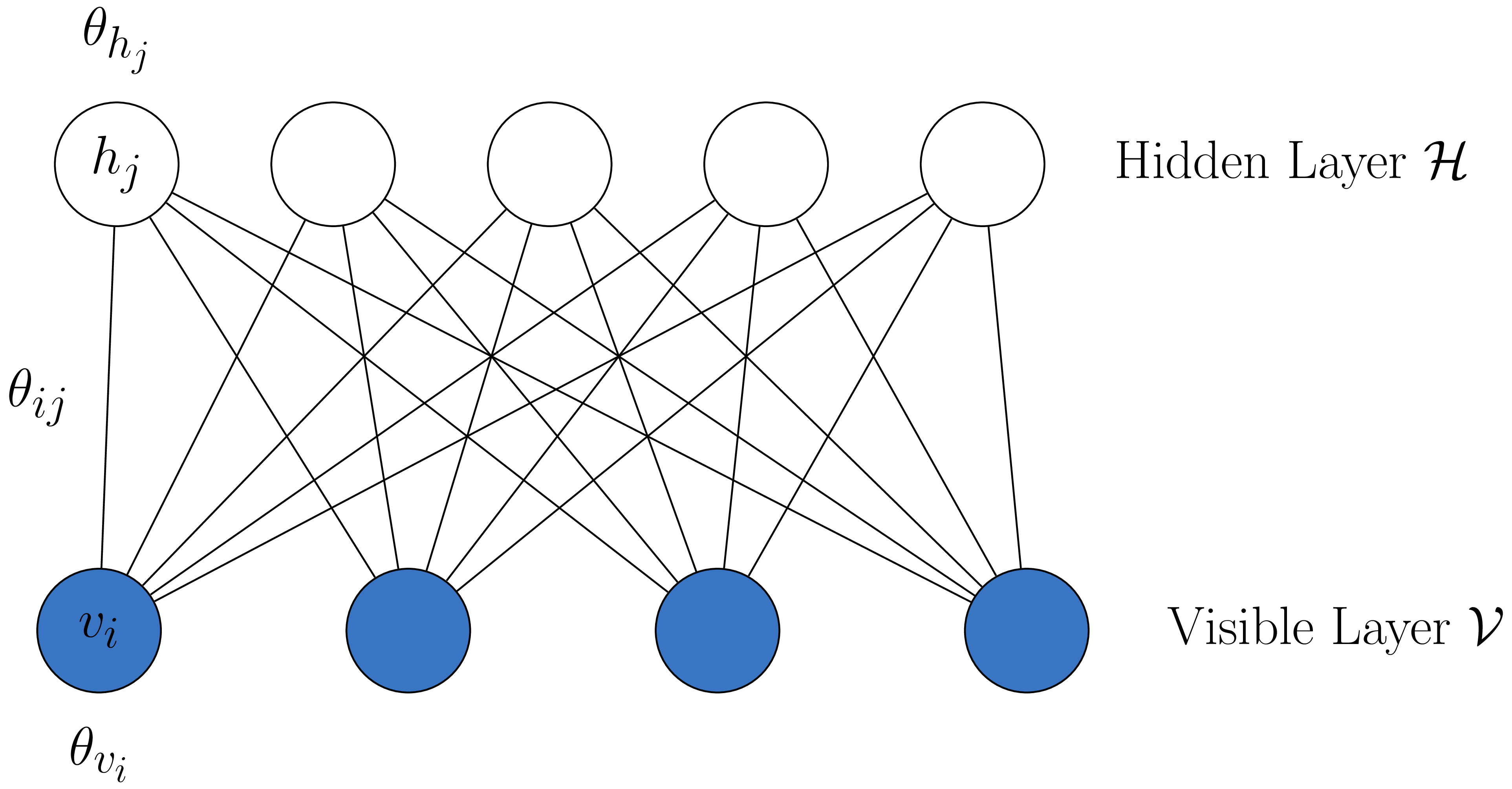
Restricted Boltzmann machine (RBM) with two layers - hidden (\(\mathcal{H}\)) and visible (\(\mathcal{V}\)) (Smolensky 1986).
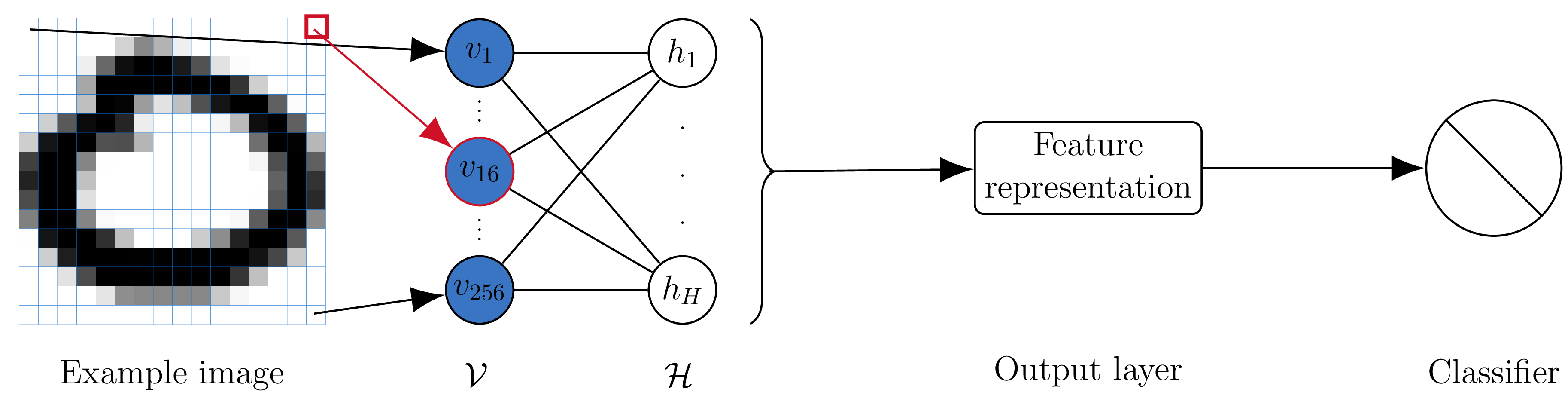 Used for image classification. Each image pixel is a node in the visible layer. The output creates features, passed to supervised learning.
Used for image classification. Each image pixel is a node in the visible layer. The output creates features, passed to supervised learning.
Let \(x = \{h_1, ..., h_H, v_1, ...,v_V\}\) represent the states of the visible and hidden nodes in an RBM. Then the probability each node taking the value corresponding to \(x\) is:
\[ f_{\theta} (x) = \frac{\exp\left(Q(x)\right)}{\sum\limits_{x \in \mathcal{X}}\exp\left(Q(x)\right)} \]
Where \(Q(x) = \sum\limits_{i = 1}^V \sum\limits_{j=1}^H \theta_{ij} v_i h_j + \sum\limits_{i = 1}^V\theta_{v_i} v_i + \sum\limits_{j = 1}^H\theta_{h_j} h_j\) denotes the neg-potentional function of the model, having support set \(\mathcal{S}\).
“Deep Boltzmann machine” - multiple single layer restricted Boltzmann machines with the lower stack hidden layer acting as the visible layer for the higher stacked model
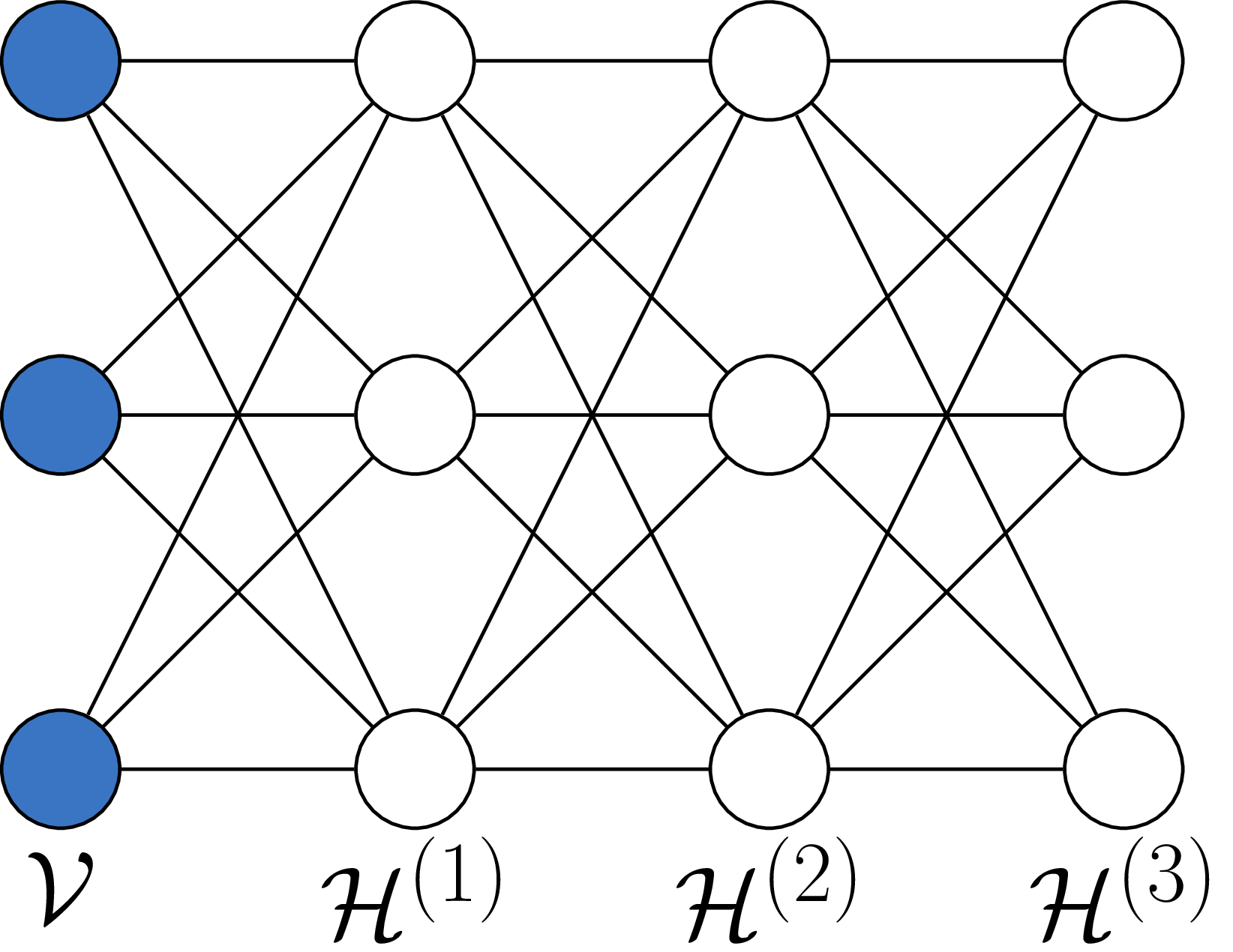
Claimed ability to learn “internal representations that become increasingly complex” (Salakhutdinov and Hinton 2009), used in classification problems.
Current heuristic fitting methods seem to work for classification. Beyond classification, RBMs are generative models:
To generate data from an RBM, we can start with a random state in one of the layers and then perform alternating Gibbs sampling. (Hinton, Osindero, and Teh 2006)
Can we fit a model that generates data that looks like data?
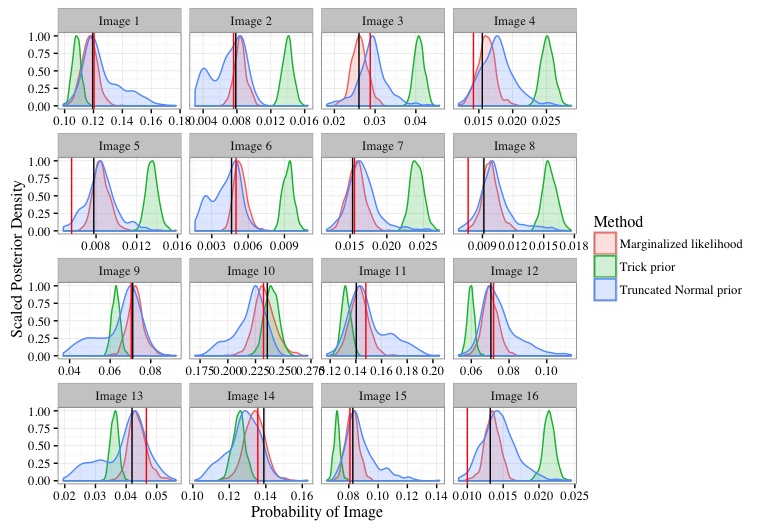
The highly flexible nature of the RBM (\(H + V + HV\) parameters) makes three characteristics of model impropriety of particular concern.
| Characteristic | Detection |
|---|---|
| Disproportionate amount of probability placed on only a few elements of the sample space by the model (Handcock et al. 2003) | If random variables in \(Q(\cdot)\) have a collective mean \(\mu(\theta)\) close to the boundary of the convex hull of \(\mathcal{S}\). |
Let \(R(\theta) = \max_{v} \max_{h}Q(x) - \min_{v}\max_{h}Q(x) - H\log 2\).
| Characteristic | Detection |
|---|---|
| Small changes in natural parameters result in large changes in probability masses, excessive sensitivity (Schweinberger 2011). | If \(R(\theta)/V\) is large, then the the maximum log-likelihood ratio of two images that differ in only one pixel is large. |
| Characteristic | Detection |
|---|---|
| Due to the existence of dependence, marginal mean-structure no longer maintained (Kaiser 2007). | If the magnitude of the difference between model expectations and expectations under independence (dependence parameters of zero), \(\left\vert E( X \vert \theta) -E( X \vert \emptyset ) \right\vert\), is large. |
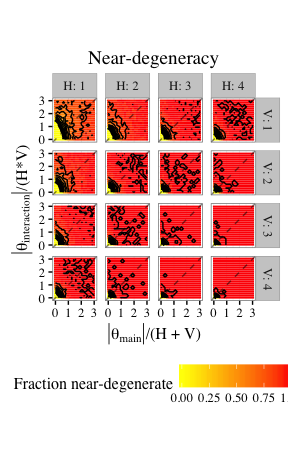
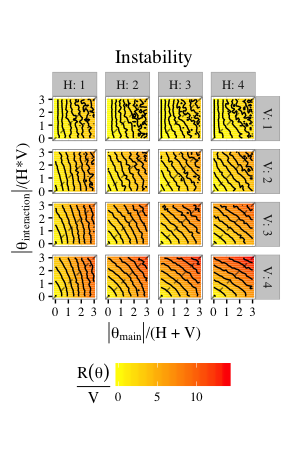
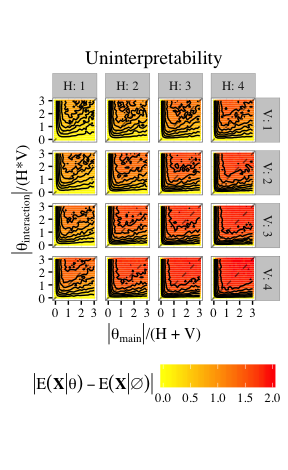 RBMs easily are near-degenerate, unstable, and uninterpretable for large portions of parameter space.
RBMs easily are near-degenerate, unstable, and uninterpretable for large portions of parameter space.
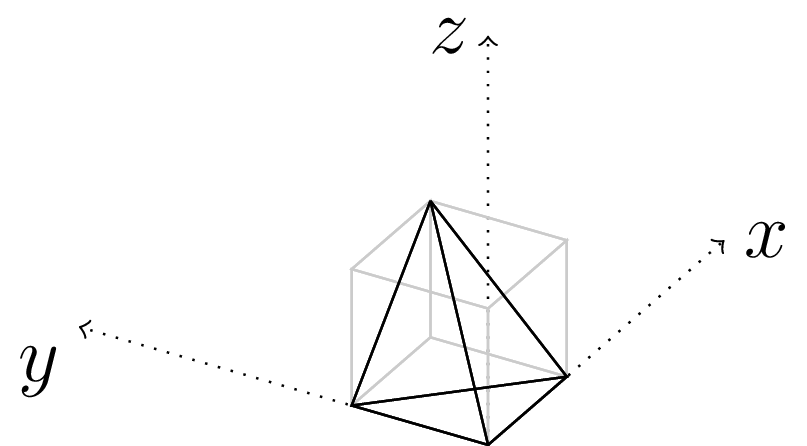

Convex hulls of the statistic space for a toy RBM with \(V = H = 1\) for \(\{0,1\}\) and \(\{-1,1\}\)-encoding enclosed by an unrestricted hull of 3-space.
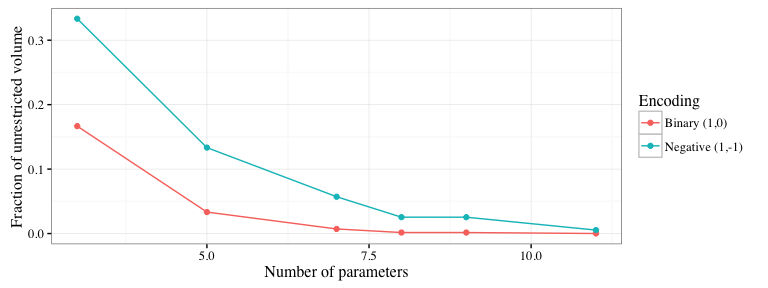
Handcock, Mark S, Garry Robins, Tom AB Snijders, Jim Moody, and Julian Besag. 2003. “Assessing Degeneracy in Statistical Models of Social Networks.” Working paper.
Hinton, Geoffrey E, Simon Osindero, and Yee-Whye Teh. 2006. “A Fast Learning Algorithm for Deep Belief Nets.” Neural Computation 18 (7). MIT Press: 1527–54.
Kaiser, Mark S. 2007. “Statistical Dependence in Markov Random Field Models.” Statistics Preprints Paper 57. Digital Repository @ Iowa State University. http://lib.dr.iastate.edu/stat_las_preprints/57/.
Li, Jing. 2014. “Biclustering Methods and a Bayesian Approach to Fitting Boltzmann Machines in Statistical Learning.” PhD thesis, Iowa State University; Graduate Theses; Dissertations. http://lib.dr.iastate.edu/etd/14173/.
Salakhutdinov, Ruslan, and Geoffrey E Hinton. 2009. “Deep Boltzmann Machines.” In International Conference on Artificial Intelligence and Statistics, 448–55.
Schweinberger, Michael. 2011. “Instability, Sensitivity, and Degeneracy of Discrete Exponential Families.” Journal of the American Statistical Association 106 (496). Taylor & Francis: 1361–70.
Smolensky, P. 1986. “Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1.” In, edited by David E. Rumelhart, James L. McClelland, and CORPORATE PDP Research Group, 194–281. Cambridge, MA, USA: MIT Press. http://dl.acm.org/citation.cfm?id=104279.104290.
Zhou, Wen. 2014. “Some Bayesian and Multivariate Analysis Methods in Statistical Machine Learning and Applications.” PhD thesis, Iowa State University; Graduate Theses; Dissertations. http://lib.dr.iastate.edu/etd/13816/.